機動學HW4

B94611023許惠善

本次作業二三僅要求畫出對應的相關位置，沒有明確表示是否要以動畫方式呈現，所以我的程式碼暫以「動畫」呈現，如果不想要以動畫呈現的話，分別在第二題的第7、第三題第8行(clf部分)行以及第二題28~34行第三題第30行處(pause部分)前，加上%使其變成註解方式，可自由改變是否以動態程式呈現，或是只要圖片亦可直接刪除上述程式碼。

另外我的螢幕因為是16:9的，所以圖形在動畫會跑得有點怪怪的，好像有點不合比例，不過我確定我的程式碼在別人電腦裡跑出來是正確無誤的。

以下為程式碼內容：

ANS1:



clf;

%宣告三角形邊長
L=23+10;

%宣告三角形的三個座標，為了回到原點我們必須對起點重複
Triangle=[0 0;L 0;L/2 (L.*3^0.5)./2;0 0];
%宣告另一個triangle，使我們可以暫存三角形的旋轉座標
triangle=Triangle;
%因為總共旋轉三次，所以使用for畫圖三次縮短程式碼
for i=1:1:3;

%本段的if i==2的部分是將第二個座標先移到原點做旋轉
%下一段i==2的部分是把座標在移回去原來對應的圖形
if(i==2);
Triangle(:,1)=Triangle(:,1)-L;
end;
%本段的if i==3的部分是將第三個座標先移到原點做旋轉
%特別要注意的是：
%但由於在第二個部分的時候我們先把Triangle(:,1)都向左移了L
%所以這部分我們只要移動向右L/2
%下一段i==2的部分是把座標在移回去原來對應的圖形
if(i==3)
Triangle(:,1)=Triangle(:,1)+L/2;
Triangle(:,2)=(Triangle(:,2)-(L.*3^0.5)./2);
end;
for theta=0:0.5:360;

%x座標旋轉
triangle(:,1)=Triangle(:,1)*cosd(theta)+Triangle(:,2)*sind(theta);

%y座標旋轉
triangle(:,2)=-Triangle(:,1)*sind(theta)+Triangle(:,2)*cosd(theta);

if(i==2);
triangle(:,1)=triangle(:,1)+L;
end;
if(i==3)
triangle(:,1)=triangle(:,1)+L/2;
triangle(:,2)=(triangle(:,2)+(L.*3^0.5)./2);
end;

axis equal;
axis ([-40 80 -40 80]);

%畫出三角形
line(triangle(:,1),triangle(:,2));

grid on;
hold on;

%使圖形暫停0.0001秒鐘，變成動畫
pause(0.0001);

%除了最後一個圖以外，我們都要清除原來的圖形，才會是動畫，
%為方便觀察每點第一圖停留較久，尤其第一點旋轉圖的第一途停留最久
if theta==0
pause(1.5);
if i==1
pause(5)
end
end
if i<3theta<360;
clf;
end;
end;
end;



Ans2:



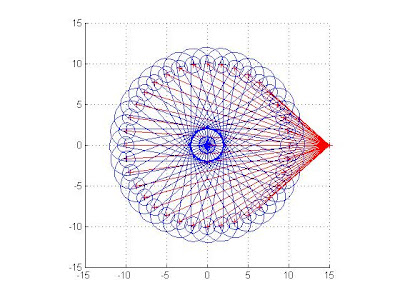
%先訂出連桿的始點
L=[0 0;10 0];
%宣告一個變數以做旋轉
l=L;
%動畫從0度到360度每隔一度做變化
for theta=0:1:360;
clf;

%x座標旋轉
l(:,1)=L(:,1)*cosd(theta)+L(:,2)*sind(theta);

%y座標旋轉
l(:,2)=-L(:,1)*sind(theta)+L(:,2)*cosd(theta);

%呼叫lineshape函數繪圖
linkshape([l(1,1),l(1,2)],[l(2,1),l(2,2)],4);
hold on;

%畫出彈簧位置與連桿連結，為了讓圖形看起來比較清楚，特別將彈簧畫紅色，並在兩端做+記號
plot(15,0,'r+')
plot(l(2,1),l(2,2),'r+')
line([15,l(2,1)],[0,l(2,2)],'color','r');


axis ([-15 15 -15 15]);
grid on;

%為了讓圖形觀察容易，在初始值的時候停留一秒鐘
if theta==0;
pause(10)
end;

pause(0.001);
end;


Ans 3:



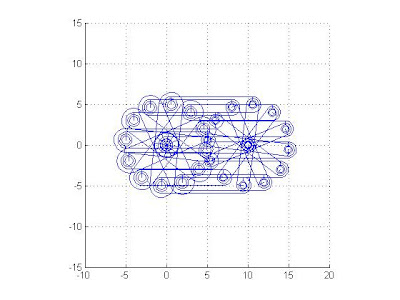
%先訂出連桿的始點
%A(0,0);B(3,4);C(13,4);D(10,0)，
L=[0 0;3 4;13 4;10 0];
%宣告一個變數以做旋轉
l=L;
%動畫從0度到360度每隔一度做變化
for theta=0:30:360;
clf;

%首先僅需考慮主動軸
%x座標旋轉
l(2,1)=L(2,1)*cosd(theta)+L(2,2)*sind(theta);
%y座標旋轉
l(2,2)=-L(2,1)*sind(theta)+L(2,2)*cosd(theta);


%因為AB是主動軸，所以C點的位置會受到B點牽制，故XC=XB+10
l(3,1)=l(2,1)+10;
l(3,2)=l(2,2);

%呼叫lineshape函數繪圖
linkshape([l(1,1),l(1,2)],[l(2,1),l(2,2)],3);
linkshape([l(2,1),l(2,2)],[l(3,1),l(3,2)],2);
linkshape([l(3,1),l(3,2)],[l(4,1),l(4,2)],1.5);
linkshape([l(4,1),l(4,2)],[l(1,1),l(1,2)],2);
hold on;

axis ([-10 20 -15 15]);
grid on;
if theta==0;
pause(10);
end;
pause(0.8);
end;

機動學HW3

Ans1:
y軸上的點為拳頭的軌跡，下方連續曲線為關節的軌跡，每個拳頭會對上一個關節的點，頭底在(0,0)的位置。

(1)程式碼

%L1=30手臂長;
%L2=25手肘長;
%H表示脖子到頭頂的高度=30,(但此處並沒有考慮到頭的寬度);

L1=30;
L2=25;
H=30;


%L也就是手整體伸長的高度;
%也就是假想拳頭的最高點;

L=L1+L2;
y=H:5:L;
x=0;
plot(x,y,'o');

%至此我們先假想了拳頭的移動;
%y由H一直移動到L;

%圖片使用hold on可以把圖形都合在一張圖上;
hold on;

%利用餘弦定律,求出頭與手肘的夾角餘弦值;
c=(y.^2+L2.^2-L1.^2)./(2.*L2*y);

%因為頭與手肘的夾角取正弦*L2就是x 座標;
%所以先做餘弦反函數再取正弦乘上L2;
%y座標則是直接乘上餘弦值;

x=L2.*sin(acos(c));
y=L2.*c;

%畫出圖形
plot(x,y,'o');
hold on;
plot(x,y);

grid on;

(2)移動的範圍
L1+L2=L為最高點
H則是最低點
(3)
假設1：
頭到手肘的底部是忽略其距離的，也就是頭是一條直線，具有高度不具寬度，亦即手完全向上伸展時，整隻手包含手肘手臂及拳頭，可以和頭頂中心上方的延長線重合。

假設2：
忽略拳頭的大小不計，視為在手臂底端的質點。

假設3：
脖子底端到手臂的高度（也就是肩膀斜度所造成的高度）忽略。

基於這三個假設可以想成移動的軌跡是(拳頭高度+頭高)、手臂、手肘三者圍成一個三角形，而拳頭到最高點的時(手肘+手臂)與(拳頭高度+頭高)兩線重合。然而我們知道這三個假設與現實不合。

[假設1]的部分會造成實際值＜我們所求的數據
[假設2]則造成實際值＞我們所求的數據
[假設3]的部分會造成實際值＜我們所求的數據。

所以可知道這個圖形僅供粗略的參考，如果想要知道實際值則要實際頭部的寬度要限制住手可以移動的軌跡，也要去考慮手的質心位置和高度，最後需要考慮的就是脖子底端和手底端真的高度差。

Ans2：日常生活應用的器材中，請舉例（圖示或照片）說明下列之分類：

（1）旋轉對
EX:門片鉸練

Def：
a.兩剛體軸同線：
說明：上下兩片門片鉸練，當兩片套在一起時，中心軸會重合。如圖所示。

b.僅有一個共同軸可供旋轉：
說明：兩門片鉸練重合後，繞中心軸旋轉。ROF=1，如圖所示


門片鉸練一片固定在門上，一片固定在門框上，其相對旋轉運動帶動了門繞著門片鉸練的中心軸旋轉而可自由開關。 以下是門從大角度關到小角度的圖片。

(2)高對與低對運動結 ：

a.高對：
EX：
突輪滾動及滑動：衣櫃抽屜

左圖是衣櫃的抽屜，上有滾輪，右圖是衣櫃裡的軌道，滾輪順著軌道由左向右移動。和課本上2.16左上角圖輪滾動及滑動之形式相同。

下方圖片為兩個和起來工作的圖片。

b.低對
C型對：小掛勾

<1>外部掛勾和中心粉紅色杆子兩軸重合在中心粉紅色杆子中心線

<2>第一圖的掛勾經過向左移，以及向上旋轉後形成第二圖的狀況。（即為一軸向平移，一垂直軸之旋轉運動）

<3>DOF=2，拘束度=4

(3)外型式閉合結或外力閉合結

a.外型式閉合結：門栓
門栓原為C型對，但門栓的限制在其外框，如圖中黃線所表示之，所以其平移的距離分別是兩圖的左右極限，而旋轉的角度限制則為向上90度。

b.外力閉合結：懸掛重物的掛勾

如圖所示，掛勾設計就是為的懸掛東西，當東西掛上後，因物體的重量，造成一向下拉的外力，所以掛勾就無法再做旋轉的動作。

Ans 3:(1程式碼及圖片)

%宣告θ from:0~360;

theta=0:1:360;

%宣告圓的半徑

r=80;

%宣告頭的半徑
rh=(r-r*cosd(60))./2

%我假設腳為半徑，腳的開叉處為圓心

%手伸展成水平，緊接在頭下方，忽略脖子

%手與腳開叉處的連線和腳開叉處與頭底的連線角度為60

%腳開叉處與腳的連線和腳開叉處與頭底的連線角度為45

%在此標出腳和手以及腳開叉處，圓心，頭圓心的未旋轉時x,y座標

Xp=[r*sind(60),-r*sind(60),-r*sind(45),r*sind(45),0,0,0];

Yp=[r*cosd(60),r*cosd(60),-r*cosd(45),-r*cosd(45),r*cosd(60),0,(r+r*cosd(60))./2]

%將這些座標值設在for外，以利我先旋轉在平移時不會變成新的座標在旋轉
%由0到360度每隔30度做一次旋轉

for times=0:30:360

%畫出人形以及頭形和大圓

line([xp(1),xp(2)],[yp(1),yp(2)],'color','red');

line([xp(5),xp(6)],[yp(5),yp(6)],'color','yellow');

line([xp(6),xp(3)],[yp(6),yp(3)],'color','black');

line([xp(6),xp(4)],[yp(6),yp(4)]);hold on;

x=xp(6)+r*cosd(theta);

y=yp(6)+r*sind(theta);

plot(x,y);

hold on;

xh=xp(7)+rh*cosd(theta);

yh=yp(7)+rh*sind(theta);

plot(xh,yh)

hold on;

%x座標旋轉

xp=Xp*cosd(times)+Yp*sind(times)

%旋轉後在平移，路徑是rθ

xp=xp+(pi*r*times)./180

%y座標旋轉

yp=-Xp*sind(times)+Yp*cosd(times)

%跳出回圈

end;

axis equal;

(2)在我的程式碼中，宣告了r也就是大圓半徑，由我的圖形可見我的身高即為我的直徑，所以你可以輸入（身高/2）當作r。當然，其中我假設腳長即為半徑長，所以只要知道該人個腳長，即可輸入大圓的半徑r。

另外我先設定了腳以及手的角度，所以如果你要更改你的手臂或是腳張開的角度，也可以更改程式碼中的(

%在此標出腳和手以及腳開叉處，圓心，頭圓心的未旋轉時x,y座標
Xp=[r*sind(60),-r*sind(60),-r*sind(45),r*sind(45),0,0,0];
Yp=[r*cosd(60),r*cosd(60),-r*cosd(45),-r*cosd(45),r*cosd(60),0,(r+r*cosd(60))./2]

)部分，

若是改變手的角度，就改變其中60的部分的角度。（包含頭的圓心座標也可以更改了），改變腳的部分則把45的部分改成你預設的值。

當然，這個程式不是真正人體的狀況，所以我們只能粗略的做計算。

第二次作業

ANS1:

本題答案其實我有找到一個非常好的網站，騎內容十分十分的詳盡，有人體各部位的骨頭的介紹，其中包含了自由度、可以活動的角度等等都十分詳盡，詳盡到我不知道怎麼摘取片段再加上寫自己的註解，所以首先提供這個網站給大家參考，http://www.pt.ntu.edu.tw/hmchai/Kinesiology/Index.htm是台大醫學系骨科的網頁。

因為題目的要求是要自己寫說明，所以我再自己從另一本書上摘路圖片以及自己配合第二章的內容另外作答一次。

首先介紹樞紐關節








膝蓋部位就是屬於樞紐關節，可以像門一樣前後轉，但無法隨意移動。也就是機動學所謂的R型對，只有一個自由度







滑動關節，是兩個平盤疊起來，可以自由的上下左右移動，我們的腳踝就是這種關節。






接下來是重要的球臼關節



在我們的肩膀和臀部屬於此種關節，可以左右移動和旋轉，一端圓形的骨骼及一端臼形骨骼組合而成，為機動學上的球對，自由度為3。

轉動關節可以做上下左右移動和轉動。
手腕的關節屬之。

鞍狀關節一端是碼鞍狀，和另一端骨骼扣在一起，可以左右移動，有兩個自由度，如下圖，像指頭底部的關節CMC的部分。

參考資料：
1.〈到人體旅行〉p106-p109，陳文君著，泛亞文化出版2005年二刷。
2.〈漢聲精選目擊者叢書5 骨架〉，溫淑真譯，民國85年五刷。
3.http://www.pt.ntu.edu.tw/hmchai/Kinesiology/Index.htm

ANS2:

首先，在討論這個題目前，我們應該要先瞭解何謂「創造」，何謂「發明」。
創造：指的是在各種不同的，正式或非正式的環境中，創建學習情境所涉及到的研究、理論和實踐。創造可以包括一系列活動，具體根據使用的設計方法而定。
發明：一種新事物或技術的首度出現。發明可以分為物件的發明及方法的發明；而物件的發明亦不限於有形的物件，無形的物件，如電腦程式、虛擬創作等亦包括在內。
兩者都是產生一有形或無形的事物，而創造涵蓋的是在學習情境中所「涉及」的，發明著重於「首度」，也就是前所未有的觀念或物品。

(圖檔自己寫的，但是我用不清楚)

發明實例：
EX1:
「生活情境中遇到不方便」法國畫家Daguerre﹙1787-1851﹚突引發一個為什麼不能想辦法把真實的情景留下來的念頭？ → 「找尋相關器材」→「無」→「找出所需設計的目標」想辦法把真實的情景留下來→「性能」把真實的情景留下→1826年發明了日光膠版→ 「機構分析，比較與選擇，修正」1839年發明了銀版照相
EX2:
「生活情境中遇到不方便」只有不會動的平面照片→ 「找尋相關器材」→「有」1885年美國的喬治.伊斯托馬﹙1854-1932﹚發明卷狀，放入捲筒內的感光膠片，→「找出所需設計的目標」欲把照片連接製成動畫→「性能」會連續播放的短片→愛迪遜於1891年發明了放映機→ 「機構分析，比較與選擇，修正」Lumiere兄弟倆的靈感，他們於1895年將愛迪遜放映機改良成投影裝置，發明了電影。

最後，我個人認為在發明與創造有一點必須牢記在心的，即是不可以為了利益而造假或是抄襲。2005年生命科學領域轟轟烈烈的「南韓黃禹錫 幹細胞研究造假」事件，黃禹錫為了個人名譽，以偽造11個胚胎幹細胞存在過的數據和照片，提供給「科學」期刊。使南韓學術界受重挫，也喪失個人在學術界的地位，桃莉羊的製造者,愛丁堡Roslin Institute 的Ian Wilmut教授甚至因為和黃禹錫合作過也被拖累騎學術地位。近期台灣也發生中興大學生化所教授張邦彥投稿到細胞（Cell）雜誌的論文，因博士班學生為了學位而造假，對台灣也是一大傷害。無論是創造與發明，尊重以及真實相信對科學都是最重要的！


參考資料：
奇摩知識http://tw.knowledge.yahoo.com/question/?qid=1405111613285
http://news.sina.com.tw/life/bcc/tw/2006-12-21/171812259321.shtml
http://www.3dollars.com.tw/MNews.asp?NID=993


ANS3:

>> M=23+10;
>> x=1:1:10;
>>y=x.^(1/M);
>> plot(x,y);xlabel('x'):ylabel('y');title('許惠善的y=f(x)圖')